Skip to main content

机器人算法 PID

串级PID​

什么是串级PID​

什么是串级PID？顾名思义就是两个串起来的PID，下面是一个双闭环的例子，外环是位置环，内环是速度环，最终的执行器是电机，电机输出产生了速度和位置；具体框图如下图所示；

PID框图1

当然执行器也可以是四轴飞行器，整体过程如下：

  • 我们在外环给定相应的位置高度，外环PID的输出就是内环PID的期望值；
  • 内环PID的输出将产生相应的油门大小，最终飞行器会产生上升的速度；
  • 内环反馈值为速度，控制相应的速度达到外环所需的速度期望值；
  • 最终外环达到期望的位置；

可能这里比较抽象，好吧，下面继续细化一下硬件的细节；PID的算法控制其实是一种无系统模型的控制，可以根据参数经验经验去调试系统；但是实际的物理对象的模型其实早就确定好了，PID的输入量和输出量的物理意义也会因为实际的被控对象而改变；换句话说，PID**的输入基本上和系统的反馈量相关，而实际的反馈量是什么，从一开始就因为系统而确定下来了**；

内环和外环的含义​

如果外环是因，那内环就是果。万物皆有因果。比如伺服控制器的三环：

  • 位置环
  • 速度环
  • 电流环

外环的变化会直接导致内环的变化，而内环是直接导致执行器变化的关键，如果这里依然使用飞行器作为例子，对于整个四轴飞行系统而言；

  1. 我们通过控制电机的电流，从而决定电机的输出扭矩；
  2. 扭矩和负载一起决定电机转速；
  3. 螺旋桨快速旋转从而产生了飞行器的升力，于是也决定了上升的速度；
  4. 最终也导致了飞行器的位置变化；

这是整个的控制过程。如果只用单环的PID去控制系统，可以在给定系统期望的情况下达到所需要的位置吗？

答案是可以。

那这样串级PID还有什么意义吗？

答案是有。

我们试想一下，如果单纯使用单环PID去控制系统。那我们看一下单环的PID系统框图；

PID框图2

我们设定了一个高度，并且希望飞行器达到预期位置高度，那么这时候系统的反馈值只有位置量；

那么飞行器是以什么样的速度去飞行？以什么样的加速度去启动？我们就无法去有效地控制飞行器的速度，让它去快速地到达期望的位置，具体位置曲线如下图所示；

img

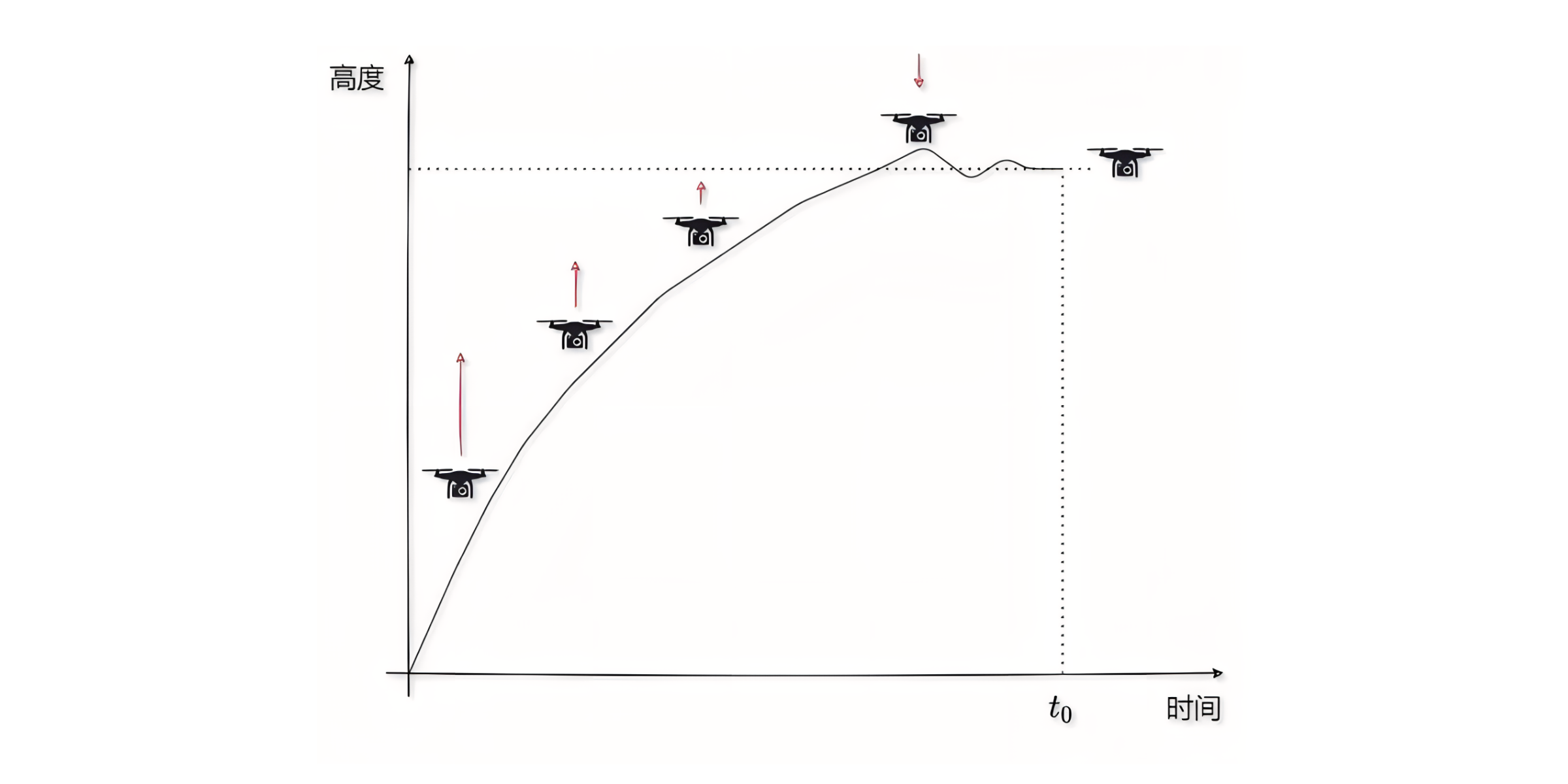
其实不难理解，因为一开始的高度差很大，所以PID计算输出的值就很大，因此初始速度会非常大，随着飞行器越来越接近期望位置，偏差越来越小，PID输出量逐渐减小，因此速度逐渐减小。

其实很多时候，PID只是底层，称之为内环PID，通过它可以先稳定某个系统，优化动态特性，然后在外层嵌套其他算法，当然，外面有好几层PID的控制系统是也很常见的。也就是我们介绍的串级PID的系统，具体如下所示；

PID框图3

控制器的本质是出入跟输出的函数映射关系。其实从这个角度来看，通常PID适用于低阶的线性时不变系统，在此基础上限制到P，I，D三个系数。

整体还需要根据具体的系统，有所变化，有的系统其实只需要两个系数（比如PD或PI），甚至有的系统只需要一个就行（比如P）。因此上面系统中，外环只需要使用P环节就足够了，另外可以对速度曲线进行规划。

假设这里使用了速度曲线规划，因为可以对飞行器的速度进行控制了；

所以我们期望它尽快达到最大速度，因此从最开始的阶段进行匀加速，达到最大速度后开始匀速上升，即将到达期望位置的时候，进行匀减速，最终悬停到目标位置；

那么整体的位置变化曲线如下所示；

img

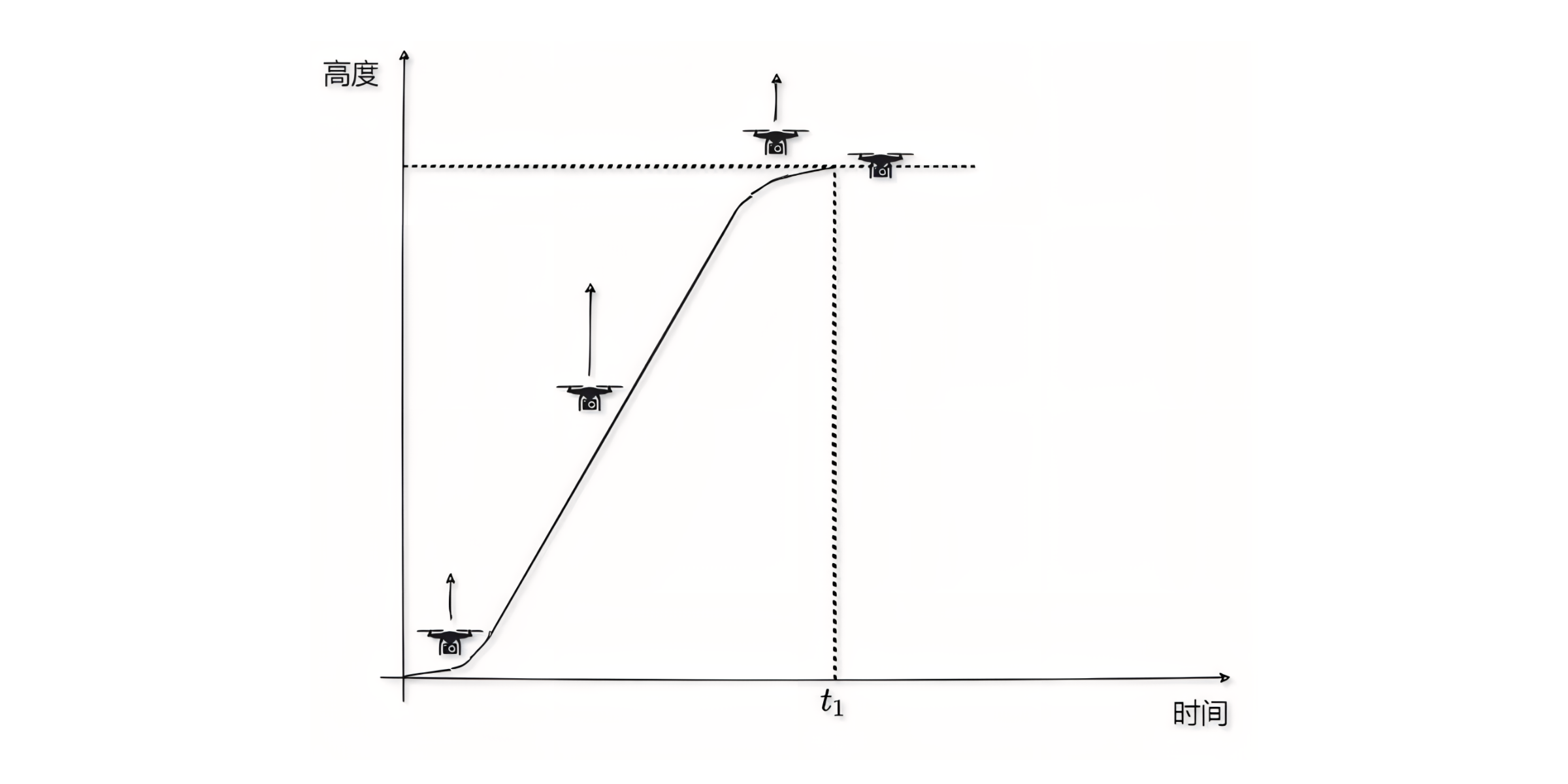
换句说话说，就是外环PID的输出作为内环PID的输入；

下面是单环PID的伪算法；

previous_error := 0  //上一次偏差
integral := 0   //积分和

//循环 
//采样周期为dt
loop:
    //setpoint 设定值
    //measured_value 反馈值
    error := setpoint − measured_value //计算得到偏差
    integral := integral + error × dt //计算得到积分累加和
    derivative := (error − previous_error) / dt //计算得到微分
    output := Kp × error + Ki × integral + Kd × derivative //计算得到PID输出
    previous_error := error //保存当前偏差为下一次采样时所需要的历史偏差
    wait(dt) //等待下一次采用
    goto loop

那么改成串级PID需要如何操作呢？

具体伪算法如下所示；

previous_error := 0  //上一次偏差
integral := 0   //积分和
previous_error_inner := 0  //内环PID上一次偏差
integral_inner := 0   //内环PID积分和
     
//循环 
//采样周期为dt
loop:
    //外环计算
    //setpoint 外环设定值
    //measured_value 外环反馈值
    error := setpoint − measured_value //计算得到偏差
    integral := integral + error × dt //计算得到积分累加和
    derivative := (error − previous_error) / (n*dt) //计算得到微分
    output := Kp × error + Ki × integral + Kd × derivative //计算得到PID输出
    previous_error := error //保存当前偏差为下一次采样时所需要的历史偏差
    setpoint_inner = output //外环的PID输出赋值给内环的PID输入     
    wait(n*dt) //等待下一次采样
 goto loop

loop_inner:       
    //setpoint_inner 内环设定值
    //measured_value_inner 内环反馈值
    error_inner := setpoint_inner − measured_value_inner //计算得到偏差
    integral_inner := integral_inner + error_inner × dt //计算得到积分累加和
    derivative_inner := (error_inner − previous_error_inner) / dt //计算得到微分
    //计算得到PID输出
    output_inner := Kp_inner × error + Ki_inner × integral_inner + Kd_inner × derivative_inner 
    previous_error_inner := error_inner //保存当前偏差为下一次采样时所需要的历史偏差
    wait(dt) //等待下一次采样
    goto loop_inner

这里将内环PID的相关变量加了后缀 _inner，loop是外环PID进行周期控制，loop_inner是内环PID进行周期控制，两者相互独立，将外环PID的输出赋值给内环PID的输入即可；遇到干扰的时候，内环控制器首先进行粗调，外环控制器再进一步细调。因此控制效果必然优于单环的PID控制系统。串级控制系统在结构上仅仅比简单控制系统多了一个内环回路，可是实践证明，对于相同的干扰，串级控制系统的控制质量是简单控制系统无法比拟的。

PID参数的意义​

串级PID的参数整定基本遵循从内到外，先整定内环PID的参数，再整定外环PID的参数；根据经验法调试参数，通常来说先整定内环比例参数P，然后整定积分参数I，动态特性可以整理微分参数D，当然还需要对饱和的情况进行处理；总之可以观察输入输出曲线；

图片

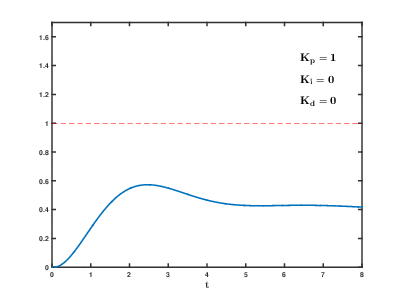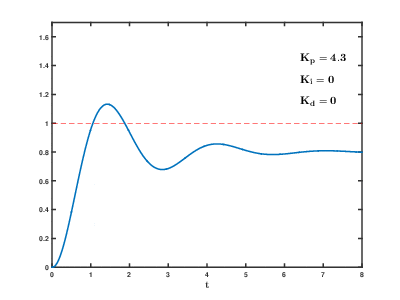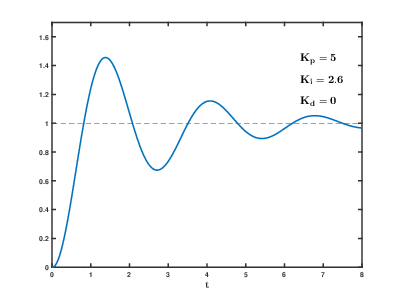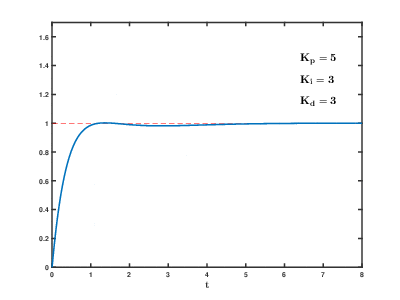
那到底什么样的响应曲线算好的呢？一般来说并不存在最优的，比如有的对速度和加速度有限制，有的系统一定不能出现超调量等等，有的系统则是响应越快越好。所以还是那句话，我不要你觉得，我要我觉得，合适才是最好的。

本文简单介绍了串级PID的相关概念，以四轴飞行器为例，对比了简单PID和串级PID的优劣。

Last updated on